corporationtore.blogg.se - Surface area of a triangular prism

SURFACE AREA OF A TRIANGULAR PRISM FREE

For example, when you cover a box in wrapping paper, then you should know its surface area to get an idea of the actual quantity of paper. Surface area is the total space available outside of an object. The base of the triangular prism is a triangle.

Surface Area of a Triangular Prism Formula A very common example of a triangular prism is the well-known chocolate box. The properties will change for irregular or semiregular polygons.A regular triangular prism has 9 edges.

Surface Area of Triangular Prism worksheets contains concept-based practice questions for students which explains the relation between net and surface area of a solid.

A triangular prism when divided has five faces, two triangular and three rectangular faces. The surface area of a right triangular prism bh + (S 1 + S 2 + h)L On substituting the values, we get SA (5 × 12) + (5 + 13 + 12) × 11 SA 60 + (30 × 11) SA 390 square units Therefore, the total surface area of a right triangular prism is 390 square units. The surface area of a triangular prism is given as A ab+3bh, where a, b and h are the side, base, and height of the prism respectively.

What are the properties of a Triangular Prism? To represent a prism, each vertex is named with a different alphabet. In brief, a triangular prism always has five faces, six vertices, and the nine edges. When edges meet together then it will make a vertex. When two faces of a Prism meet together, then it will make a line segment that is named as the edge.

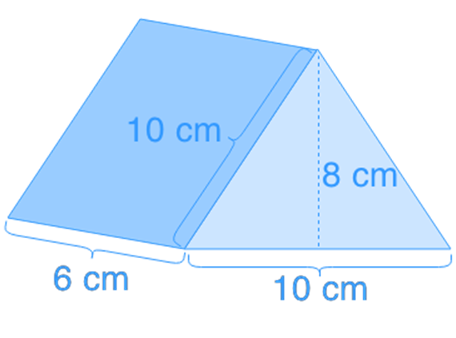
In this way, a triangular prism will be divided into five faces two triangular and three rectangular faces. The three rectangles will be named as lateral faces. Surface Area of Triangular Prism Height (H): Side1 (S1): Side2 (S2): Side3 (S3): Formula: Surface Area (B × H) + (S1 + S2 + S3) × H Where. The top and bottom of the shape are still triangular bases. We will introduce the appropriate formulae for these calculations and. When 3-dimensional shaped are formed by 2-dimensional shapes then it will be named as faces. In this lesson, students will calculate the surface area of triangular prisms. It will be divided into two rectangles and three triangles when divided properly. If you will cut the Triangular Prism into parts and put it flat on the table then you will better understand the structure of the shape. Example 1įind the surface area of a closed box with base width 3 cm, base length 5 cm and height 4 cm. Choose from 500 different sets of Surface Area of a Triangular Prism flashcards on Quizlet.

SURFACE AREA OF A TRIANGULAR PRISM FREE

To find the surface area of a rectangular prism or a box, we first flatten it creating the net, and then work out the total surface area by adding the areas of the individual rectangles. Learn Surface Area of a Triangular Prism with free interactive flashcards. The surface area of a prism is the sum of the areas of its faces. Step 3: Find the area of the rectangular sides by multiplying the perimeter of a base triangle by the length of the prism: A(b1+b2+b3)l A ( b 1 + b 2 + b 3 ). Source: Australian Curriculum, Assessment and Reporting Authority (ACARA) Solve problems involving the surface area and volume of right prisms (ACMMG218)Ĭalculate the surface area and volume of cylinders and solve related problems (ACMMG217)